#include void main() { struct sungjuk { int hakbun; char name[10]; int kor,eng,mat,total; float avg; }; sungjuk kim={10220,"kim",1,2,3}; sungjuk lee={10221,"lee",3,4,5}; kim.total=kim.kor+kim.eng+kim.mat; lee.total=lee.kor+lee.eng+lee.mat; kim.avg=kim.total/3; lee.avg=lee.total/3; printf("%d 이름 : %s | 국어[%d] 영어[%d] 수학[%d] 총점[%d] 평균[%.2f]\n",kim.hakbun,kim.name,kim.kor,kim.eng,kim.mat,kim.total,k..
#include #include char* strcat(char *c, char *m); void main() { char *c=(char*)malloc(50); char *m=(char*)malloc(50); scanf("%s",c); scanf("%s",m); printf("%s\n",strcat(c,m)); } char* strcat(char *c, char *m) { char *re=c; while(*c!='\0') { c++; } while(*m!='\0') { *c++ = *m++; } *c='\0'; return re; }
#include int linear_search(int array[],int count,int key); void main() { int i,key,find,count; int array[]={15,12,22,30,17,25,5,7,52,32,55}; count=sizeof(array)/sizeof(int); printf("배열 array[] : "); for(i=0;i 0) printf("array[%d] = %d\n",find-1,array[find-1]); else printf("없자나\n"); } int linear_search(int array[],int count,int key) { int find; for(int i=0;i
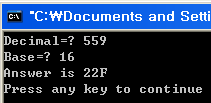
#include void main() { int b,n,i=99; char c[17]="0123456789ABCDEF",result[100]; printf("Decimal=? "); scanf("%d",&n); printf("Base=? "); scanf("%d",&b); // result[] 마지막 위치에 Null 문자 넣기 result[i]='\0'; // i=99 while(n!=0) { result[--i]=c[n%b]; // result[]
확대 형 변환( Small -> Big )자동으로 변환되고 '묵시적 형 변환' 이라고도 한다.Ex) byte b = 10; int i = b; 축소 형 변환( Big -> Small )강제로 변환해야하고 '명시적 형 변환' 이라고도 한다.Ex) int i = 10; byte b = (byte)i; 축소 형 변환의 경우에 데이터가 상실될 가능성이 있다.
#include void main() { int left, mid, right, i,j, cnt, find=0,min, index,q=0; int num[] = {2,10,3,4,5,6,13,8,9}; cnt = sizeof(num)/sizeof(int); // 배열의 크기 탐색 // 배열 정렬 for ( i = 0; i num[j] ) { min = num[j]; index = j; } } num[index] = num[i]; num[i] = min; } left = 0; right = cnt; for(i=0;i
콜라츠의 추측? 콜라츠 추측 (Collatz conjecture)은 1937년에 처음으로 이 추측을 제기한 로타르 콜라츠의 이름을 딴 것으로 3n+1 추측, 울람 추측, 혹은 헤일스톤(우박) 수열 등 여러 이름으로 불린다. 콜라츠 추측은 임의의 자연수가 다음 조작을 거쳐 항상 1이 된다는 추측이다. 짝수라면 2로 나눈다. 홀수라면 3을 곱하고 1을 더한다. 1이면 조작을 멈추고, 1이 아니면 첫 번째 단계로 돌아간다. 예를 들어, 6 에서 시작한다면, 차례로 6, 3, 10, 5, 16, 8, 4, 2, 1 이 된다. 또, 27에서 시작하면 무려 111번을 거쳐야 1이 된다. 77번째에 이르면 9232를 정점으로 도달하다가 급격히 감소하여 34단계를 더 지나면 1이 된다. 이 추측은 컴퓨터로 17 × 2..
